Uma extensão espaço tempo simétrica da mecânica quântica
Here, I will present you the spacetime symmetrical formalism of non relativistic quantum mechanics.
- Futuras aplicações no problema do tempo de travessia
- 1. Introdução
- 2. Breve demonstração do Argumento de Pauli
- 3.introduzindo notações úteis
- 4. Teoria de Extensão da MQ espaço-tempo-simétrica
- 5. Derivação de uma equação dinâmica para $\phi(t,x)$
- 6. Primeira tentativa de evolução numérica com experimento de tempo de tunelamento
- 7. Desenvolvimento analítico para solução da equação de Schroedinger espaço condicional
Heisenberg introduziu em 1924 as seguintes relações de incerteza, referentes a Heisenberg Picture of quantum mechanics:
$$ \Delta x \Delta p \geqslant \frac{\hbar}{2} \tag{1.1} $$
$$ \Delta E \Delta t \geqslant \frac{\hbar}{2} \tag{1.2} $$
Dos nossos conhecimentos prévios de mecânica quântica, sabemos que da equação $(1.1)$ existem operadores $x$ e $p$ tais que
$$ P \left | p \right \rangle = p \left | p \right \rangle \tag{1.4} $$
também que tanto $\Delta x$ como $\Delta p$ podem ser interpretados como o desvio padrão dos valores esperados de seus respectivos operadores:
$$ \Delta x = \sqrt{\left \langle x^2 \right \rangle - \left \langle x \right \rangle^2} \tag{1.5} $$
$$ \Delta p = \sqrt{\left \langle p^2 \right \rangle - \left \langle p \right \rangle^2} \tag{1.6} $$
Mas, reside na equação $(1.3)$ um problema a anos apontado pelo próprio pauli. Sabemos dos postulados de Heisenberg na mecânica quântica que a relação de comutação entre $x$ e $p$ é:
$$[X,P]= i \hbar \tag{1.7} $$
Daí, surge a pergunta então: se interpretarmos $\Delta E$ como o desvio padrão do valor esperado do operador Hamiltoniano, teremos
$$ \Delta E = \sqrt{\left \langle H^2 \right \rangle - \left \langle H \right \rangle^2} \tag{1.9} $$
Então, será possível então expressar T em forma de uma variável dinâmica, ou seja, introduzir um operador T de modo que $\Delta t$ passaria a ser interpretado como o desvio padrão do valor esperado de T?
Como já referênciamos, Pauli demonstrou que a implementação de um operador temporal na mecânica quântica faria com que a Heisenberg Picture levasse a absurdos físicos (e.g ausência de valores limitantes inferiores a um Hamiltoniano) como demonstraremos a seguir:
No regime proposto na sessão anterior, descrevemos as seguintes condições:
Vamos então agora mostrar que o estado $ \exp[i E^\prime T/\hbar] \left | E \right \rangle $ é um autoestado do operador Hamiltoniano H, com autovalor de energia $ E - E^\prime $. Comecemos expandindo o operador exponencial em formato de série:
$$ e^{iE^\prime T/\hbar} = \sum_{n=0}^{\infty} \frac{1}{n!} \left( \frac{iE^\prime T}{\hbar} \right)^n \tag{2.1} $$
Aplicando então o operador hamiltoniano pela esquerda vamos obter que,
$$ H e^{iE^\prime T/\hbar} = \sum_{n=0}^{\infty} \frac{1}{n!} H \left( \frac{iE^\prime T}{\hbar} \right)^n \tag{2.2} $$
Agora, precisamos passar o operador hamiltoniano para a direita do operador tempo. Para isso, note que
$$HT = TH + [H,T] = TH + i\hbar \tag{2.3}$$
Onde usamos então o fato de que o teorema de Pauli supoem que $[H,T] = i\hbar$. Assim aplicando então o operador $T$ pela direita em $(2.3)$ vamos obter que
$$HT^2 = THT + i\hbar T \tag{2.4}$$
E utilizando recursivamente a equação $(2.3)$ agora no primeiro termo de $(2.4)$ é fácil ver que
$$HT^2 = T^2H + 2i\hbar T \tag{2.5}$$
De maneira similar, podemos seguir então indutivamente tal
$$HT^3 = T^3H + 2i\hbar T^2 \tag{2.6}$$
Até obtermos a forma generalizada, que a esta altura espero já estar clara como sendo
$$HT^n = T^nH + 2i\hbar T^{n-1} \tag{2.7}$$
Portanto, substituindo $(2.7)$ de volta em $(2.2)$ ,
$$ H e^{iE^\prime T/\hbar} = \sum_{n=0}^{\infty} \frac{1}{n!} H \left( \frac{iE^\prime T}{\hbar} \right)^n T^nH + 2i\hbar T^{n-1} $$
$$ = e^{iE^\prime T/\hbar}H - \sum_{n=1}^{\infty} \frac{E^\prime}{n-1!} \left( \frac{iE^\prime T}{\hbar} \right)^{n-1} \tag{2.8} $$
logo,
$$ H e^{iE^\prime T/\hbar} = e^{iE^\prime T/\hbar}(H - E^\prime) \tag{2.9}$$
que nos permite concluir finalmente que:
$$ H e^{iE^\prime T/\hbar}\left | E \right \rangle = e^{iE^\prime T/\hbar} (E - E^\prime)\left | E \right \rangle $$
$$= (E - E^\prime)e^{iE^\prime T/\hbar}\left | E \right \rangle\tag{2.10}$$
Onde podemos então concluir o seguinte absurdo: a aplicação do operador unitário exponencial sugerido (que físicamente representa um deslocamento de $-E^\prime$ na energia apenas) com um $E^\prime \in \mathbb{R}$ no autoestado de energia $\left | E \right \rangle$ do operador $H$ produz um novo autoestado de energia com autovalor $E - E^\prime$. Portanto, $E - E^\prime$ pode tomar qualquer valor em $\mathbb{R}$, i.e. dado um autovalor de energia $E$, podemos sempre escolher um valor para $E^\prime$ de forma a acessar qualquer autoestado com energia $E - E^\prime \in \mathbb{R}$ desejado. Assim, vemos que se este operador existir o espectro de energias do hamiltoniano se estenderia continuamente em $(-\infty, \infty)$ independente do sistema físico, permitindo assim a criação de moto-perpetuos de energia.
Seja $P_I (i) \equiv$ densidade de probabilidade da variável $I$ ter um valor entre $i$ e $i + di$
Desta forma, a probabilidade da variável $I$ tervalor entre $(a,b)$ será de:
$$p(a,b) = \int_{a}^{b} P_I (i) di \tag{3.1} $$
Vamos tratar como sendo a probabilidade de obter $i$ dado que $j$ aconteceu como sendo $P_I(i|j) \equiv$ Função de distribuição de probabilidade (F.D.P.) da variável $I \in [i, i + di]$ quando $ J = j $. Clique aqui para mais informações
No caso de tratarmos um sistema de duas variáveis, faremos tal que $P_{I,J}(i,j) \equiv $ F.D.P das variáveis $I \in [i, i + di]$ e $J \in [j, j + dj]$ , então,
$$p(a,b;c,d) = \int_{a}^{b} di \int_{c}^{d} dj P_{I,J}(i,j) \tag{3.2} $$
Do famoso e tão usado Teorema de Bayes, vamos usar que em condições de ergodicidade temos que:
$$ P_{I,J}(i,j) = P_I(i|j) P_J(j) = P_J(j|i) P_I(i) \tag{3.3}$$
Note aqui que o fato de propormos definições baseadas em ergodicidade impõem um simetria completa entre $I$ e $J$. Note aqui que, usando as 3 ferramentas estatísticas apresentadas, já podemos criar um gancho de raciocínio para a próxima sessão. Como vamos finalmente aplicar esses conteúdos na mecânica quântica?
Vamos traduzir agora para palavras a nossa famosa equação da mecânica quântica:
$$|\psi(x,t)|^2 = |\langle x | \psi (t) \rangle|^2 \tag{3.4}$$
Como sendo a densidade de probabilidade de detectarmos uma particula na posição x dado que a medição ocorreu no instante t. Em outras palavras
$$P_{X,T}(x,t) \equiv \mathcal{P} (x,t)$$
$$P_{X}(x|t) \equiv |\psi(x,t)|^2$$
$$P_{T}(t) \equiv f(t)$$
Será que podemos então construir uma simetriz através do Teorema de Bayes?
$$ \mathcal{P}(x,t) = P_T(t|x)P_X(x) = P_X(x|t)P_T(t) $$
Vamos então na sessão que segue, no intuito de contornar o argumento de Pauli, sair do espaço de Hilbert $\mathcal{H_x}$ que define a posição como variável dinâmica e o tempo como parâmetro apenas, que é o espaço onde ocorre a catástrofe da energia quando tentamos introduzir um operador tempo que seja canônicamente conjugado com $H$, e vamos agora para um espaço $\mathcal{H_t}$ onde a criação de um operador $T$ não é mais catastrófica. A intenção é que os espaços futuramente se relacionem através da seguinte transformação
$$ \mathcal{H} \equiv \mathcal{H_X} \otimes \mathcal{H_T} \tag{3.6}$$
Pretendemos enxergar então através da relação $\Delta E \Delta t \geqslant \frac{\hbar}{2}$ que o termo $\Delta t$ representa então a incerteza de sucessivas medições do operador $T$.
No intuito de prover uma fundamentação teórica mais completa, vamos construir esse desenvolvimento a partir do zero. Uma das operações binárias mais importantes no tocante a teoria da mecânica clássica Hamiltoniana são os conhecidos Colchetes de Poisson. Relembre que os definimos da seguinte forma:
$$ \{\lambda, \omega\} = \sum_{k}^{N} \left( \frac{\partial \lambda}{\partial q_k}\frac{\partial \omega}{\partial p_k} - \frac{\partial \lambda}{\partial p_k}\frac{\partial \omega}{\partial q_k}\right) \Rightarrow \tag{4.1}$$
$$\Rightarrow \{q_i, p_j\} = \sum_{k}^{N} \left( \frac{\partial q_i}{\partial q_k}\frac{\partial p_j}{\partial p_k} - \frac{\partial q_i}{\partial p_k}\frac{\partial p_j}{\partial q_k}\right) = \sum_{k}^{N} \delta_{ik}\delta_{jk} = \delta_{ij}$$
$$\Rightarrow \{q_i, q_j\} = \sum_{k}^{N} \left( \frac{\partial q_i}{\partial q_k}\frac{\partial q_j}{\partial p_k} - \frac{\partial q_i}{\partial p_k}\frac{\partial q_j}{\partial q_k}\right) = 0 $$
$$\Rightarrow \{p_i, p_j\} = 0 $$
Onde temos então definidos os colchetes de poisson, e pontuadas suas propriedades mais diretas:
$$\{q_i, p_j\} = \delta_{ij} ; \{q_i, q_j\} = \{p_i, p_j\} = 0; \tag{4.2} $$
E fácil então agora reescrever a partir dos colchetes de poisson as equações de Hamilton, de forma que:
$$ \dot{q_i} = \{q_i, \mathcal{H}\}; \tag{4.3}$$
$$ \dot{p_i} = \{p_i, \mathcal{H}\}; \tag{4.4}$$
Sejam então $(q,p) = (q_1,...,q_n; p_1,...,p_n)$ o conjunto de coordenadas necessárias para descrever um sistema, existe então também um $(\bar{q},\bar{p}) = (\bar{q_1},...,\bar{q_n}; \bar{p_1},...,\bar{p_n})$ que o descreve.
$$\begin{matrix} (q,p) & \rightarrow & (\bar{q},\bar{p}) \\ \downarrow & & \downarrow \\ \mathcal{H}(q,p) & \rightarrow & \mathbb{K}(\bar{q},\bar{p}) \\ \end{matrix}$$
Se tivermos então as equações de Hamilton para este novo sistema de coordenadas, isto é,
$$ \dot{\bar{q_i}} = \{\bar{q}, \mathbb{K}\}; \tag{4.5}$$
$$ \dot{\bar{p_i}} = \{\bar{p}, \mathbb{K}\}; \tag{4.6}$$
Essa transformação então é dita canônica, o que acarreta diretamente em
$$\{\bar{q_i}, \bar{p_j}\} = \delta_{ij} ; \{\bar{q_i}, \bar{q_j}\} = \{\bar{p_i}, \bar{p_j}\} = 0; \tag{4.7} $$
Podemos então agora escolher uma função geradora $\delta$ de modo a nova hamiltoniana $\mathbb{K}$ seja identicamente nula, e isso nos leva a equção de Hamilton-Jacobi:
onde temos que
Buscando uma motivação de visão ondulatória da já desenvolvida e consolidada mecânica clássico (como em paraleleo desenvolvido para a ótica), vamos buscar enxergar $S$ como uma fase de um processo ondulatório de um regime físico qualquer, isto é,
$$\psi = exp\left({\frac{iS}{\hbar}}\right) \Rightarrow ln(\psi) = \frac{iS}{\hbar} \Rightarrow S = -i \hbar ln\psi $$
Isto é,
$$\frac{\partial S}{\partial t} =-i \hbar \left( \frac{1}{\psi}\frac{\partial \psi}{\partial t}\right) ,\frac{\partial S}{\partial q} =-i \hbar \left( \frac{1}{\psi}\frac{\partial \psi}{\partial q}\right) \tag{4.10}$$
Substituindo esses resultados nas equações (4.8) e (4.9) vamos obter
$$\mathcal{H} \psi = i\hbar \frac{\partial \psi}{\partial t} \tag{4.11}$$
$$p \psi = i\hbar \frac{\partial \psi}{\partial q} \tag{4.12}$$
Especificamente essas relações são de nosso grande interesse. Note que elas se assemelham ás equações da dinâmica de evolução de $|\psi \rangle$
Equação de Schroedinger: $$ \mathcal{H} |\psi \rangle = i\hbar \frac{\partial |\psi \rangle}{\partial t} \tag{4.13}$$
Operador momento atuando em $\mathcal{H_x}$: $$ \langle \psi | p |\psi \rangle = -i\hbar \frac{\partial \psi}{\partial t} \tag{4.14}$$
E elas assim o fazem pelo postulado de coerência entre a MQ e a MC direto do Heisenberg picture.
$$ \mathcal{H} |\psi(t) \rangle = i\hbar \frac{\partial |\psi (t) \rangle}{\partial t} $$
$$ \langle x | \hat{p} |\psi(t) \rangle = -i\hbar \frac{\partial \psi (x,t)}{\partial x} $$
$$ x, P, \hat{h}, \hat{T}$$
$$ \mathcal{P} |\phi(x) \rangle = -i\hbar \frac{\partial |\phi (x) \rangle}{\partial x} $$
$$ \langle t | \hat{h} |\phi(t) \rangle = i\hbar \frac{\partial \phi (x,t)}{\partial t} \tag{4.14}$$
Na nossa formulação alternativa, o equivalente a equação de Schroedinger vai ser dito o "pamiltoneano", sendo ela uma espécie de segunda lei de Newton para nossa nova formulação.
$x$ agora será tratado como um parâmetro, $t$ como um autovalor associado a $\hat{t}$, e as variáveis canônicamente conjugadas agora fazem com que
$$[ \hat{h},\hat{t} ]= i \hbar$$
Essa formulação alternativa se mostra então tão poderosa quanto a mecânica quântica tradicional, mas é capaz de possibilitar a obtenção de resultados antes inacessiveís; Nada mais justo então do que reafirmar a transformação que propuzemos anteriormente em (3.6):
$$ \mathcal{H} \equiv \mathcal{H_X} \otimes \mathcal{H_T}$$
de forma que:
$$\mathcal{H_x} \rightarrow | \psi \rangle $$
$$\mathcal{H_t} \rightarrow | \phi \rangle $$
$$\mathcal{H} \rightarrow | \Psi \rangle $$
Desta forma, vamos tratar o produto interno dentro desse espaço como sendo:
$$|| \Psi \rangle = \int_{\mathcal{}H_T} dt \int_{\mathcal{}H_X} dx |x t \rangle \Psi(x,t) \tag{4.15}$$
Onde de $\Psi(x,t) \rightarrow |\Psi|^2 = \mathcal{P}(x,t)$.
usando o teorema de Bayes: $$ \mathcal{P}(x,t) = P_X(x|t)P_T(t) = P_T(t|x)P_X(x) $$
$$ |\Psi (x,t)|^2 = |\psi (x,t)|^2 f(t) = |\phi (t,x)|^2 g(x) $$
$$ \Psi (x,t) = \psi (x,t) \sqrt{f(t)} = \phi (t,x)\sqrt{g(x)} $$
$$ \Psi^* (x,t) = \psi^* (x,t) \sqrt{f(t)} = \phi^* (t,x) \sqrt{g(x)} $$
Isto é, finalmente, o que buscavamos,
$$ |x t \rangle \equiv |x\rangle \otimes |t\rangle $$
No mais, já que sabemos que $ \mathcal{H} \equiv \mathcal{H_X} \otimes \mathcal{H_T}$, devemos saber como atuam os operadores num autoket de $ \mathcal{H}$
$$\langle xt | \hat{p} |\Psi \rangle = \langle xt |\hat{p} \int dx^\prime \int dt^\prime \Psi(x^\prime,t^\prime) |x^\prime t^\prime \rangle $$
$$ = \int dx^\prime \int dt^\prime \Psi(x^\prime,t^\prime) \langle xt |\hat{p}|x^\prime t^\prime \rangle $$
$$ = \int dx^\prime \int dt^\prime \Psi(x^\prime,t^\prime) \langle t | t^\prime \rangle \langle x |\hat{p}|x^\prime \rangle $$
$$ =\int dt^\prime \langle t | t^\prime \rangle \int dx^\prime \Psi(x^\prime,t^\prime) \langle x |\hat{p}|x^\prime \rangle $$
$$ =\sqrt{f(t)} \int dx^\prime \Psi(x^\prime,t^\prime) \langle x |\hat{p}|x^\prime \rangle $$
$$ =\sqrt{f(t)} \langle x| \hat{p} \int dx^\prime \Psi(x^\prime,t^\prime) |x^\prime \rangle $$
$$\Rightarrow \langle xt | \hat{p} |\Psi \rangle = \sqrt{f(t)} \langle x| \hat{p} |\psi(t) \rangle $$
Analogamente, também é idêntico ver que,
$$\Rightarrow \langle xt | \hat{h} |\Psi \rangle = \sqrt{g(x)} \langle t| \hat{h} |\phi(x) \rangle $$
Dada a construção de raciocinio até então, temos em nosso conhecimento que:
- Equação de Schroedinger tempo-condicional:
$$ \mathcal{H} |\psi(t) \rangle = i\hbar \frac{\partial |\psi (t) \rangle}{\partial t} \tag{5.1}$$
temos aqui o tempo como parâmetro, e a equação trata de uma evolução temporal do ket $\psi$.
- Equação de Schroedinger espaço-condicional:
$$ \mathcal{P} |\phi(x) \rangle = -i\hbar \frac{\partial |\phi (x) \rangle}{\partial x} \tag{5.2}$$
Agora, a posição é que será tratada como parâmetro, e a equação trata de uma evolução espacial do ket $\phi$.
Resta agora explicitar as transformações que envolvem o nosso novo operador Pamiltoniano $(\mathcal{P})$, para isso iremos utilizar mais uma vez o formalismo Hamiltoniano da mecânica clássica como uma analogia para a construção da teoria.
Do fomrmalismo tradicional, temos que $$\mathcal{H}(q, p; t) = \frac{p^2}{2m} + V(x,t) \Rightarrow H (X, \hat{p};t) = \frac{\hat{p}^2}{2m} + V(x,t) \tag{5.3}$$
Podemos então isolar $p$ na equação acima e explicitá-lo em função de $\mathcal{H}$ e $V$
$$p(t, \mathcal{H};x) = \pm \sqrt{2m} (\mathcal{H} - V(t,x))^{1/2}$$
$$\Rightarrow P(T, \hat{h};x) = \hat{\sigma_z} \sqrt{2m} (\hat{h} - V(T,x))^{1/2}\tag{5.4}$$
Aplicando na equação de Schroedinger espaço condicional que desenvolvemos anteriormente, temos que
$$\sqrt{2m} \hat{\sigma_z} [\hat{h} - V(T,x)]^{1/2} |\phi (x) \rangle = -i \hbar \frac{d}{dx} | \phi (x) \rangle \tag{5.5}$$
Note que ao projetarmos em $\langle t |$, vamos obter que
$$\sqrt{2m} \hat{\sigma_z} [i \hbar \frac{\partial}{\partial t} - V(T,x)]^{1/2} \phi (t,x) = -i \hbar \frac{\partial}{\partial x} \phi (t,x) \tag{5.6}$$
O caráter matricial de $\hat{\sigma_z}$ é resultado apenas da definição dos dois polos da raíz $$\phi(t,x) = \begin{pmatrix} \phi^+ (t,x) \\ \phi^- (t,x) \\ \end{pmatrix} \tag{5.7}$$
Onde $\phi^+$ é a amplitude de porbabilidade da partícula incidir em um sentido no aparato localizado $x$, e $\phi^-$ no outro sentido. Claro que se $\rho (t,x)$ for a densidade total
$$\rho (x,t) = |\phi^+|^2 + |\phi^-|^2 = \phi^{\dagger} \phi \tag{5.8}$$
Da formulação tradicional, sabemos que $|\psi (x,t)|^2 = |\langle x | \psi(t) \rangle|^2 \rightarrow$ equivale a densidade de probabilidade de detectarmos a partícula na posição x, dado que a medição ocorreu no instante t. Agora, nossa proposta chegou ao ponto de nos fornecer o ansatz de que $|\phi (t,x)|^2 = |\langle t | \phi(x) \rangle|^2 $, é a relação complementar dentro da nossa teoria estendida que nos fornece a densidade de probabilidade de detectarmos a partícula num instante de tempo t, dado que a medição ocorreu no espaço x.
Esse desenvolvimento nos permite então evoluir temporalmente a equação de Schroedinger Bayes-simétrica no espaço $\mathcal{H_t}$, e obter então uma previsão analítica do comportamento do tempo de tunelamento em um experimento para determinar o tempo de tunelamento, como faremos computacionalmente na sessão à seguir, e compararemos com alguns artigos já publicado que se propõe a efetuar esse experimento.
Tomando como partida o exercício 4.10 sugerido pelo livro do Foot de física atômica, vamos evoluir a equação de Schroedinger a partir do seguinte script em python
import numpy as np
import matplotlib.pyplot as plt
import scipy as sp
Chamando as seguintes constantes para parametrizar nosso problema, e definindo as condições iniciais para determinar o tempo de travessia
N = 100
Am = 1
step = 0.2
E = -0.25
t = [0 for x in range(N)]
t[0] = 0.2
Vt = [0 for x in range(N)]
phi = [0 for x in range(N)]
phi[0] = 5
Usando como método de aproximação para o calculo numérico o seguinte procedimento para resolver a EDO e finalmente evoluir a nossa equação de Schroedinger como desejado: $$\frac{d f}{d t} = \frac{f(t + \delta/2)+f(t - \delta/2)}{\delta} \tag{6.1}$$
$$\frac{d^2 f}{d t^2} = \frac{f(t + \delta)+f(t - \delta)- 2f(t)}{\delta^2} \tag{6.2}$$
onde implementamos então esse algoritmo na nossa relação para $\phi(t,x)$ desenvolvido na sessão anterior
$$\sqrt{2m} \hat{\sigma_z} [\hat{h} - V(T,x)]^{1/2} |\phi (x) \rangle = -i \hbar \frac{d}{dx} | \phi (x) \rangle$$
de forma que a dependência no espaço que vai estar relacionada na solução ao fator $\exp[\frac{-iEx}{\hbar}]$ vai sempre se cancelar quando construirmos quantidades de relvância física ($|\phi|^2$) logo todas as probabilidades e valres esperados são constantes neessa grandeza
for n in range (1,N):
t[n] = t[n-1] + step
Vt[n] = -(2/t[n-1]) + (Am*(Am+1)/(t[n-1]*t[n-1]))
phi[n] = (2*phi[n-1]+(Vt[n-1] - E)*phi[n-1]*step*step - (1-step/t[n-1])*phi[n-2])/(1+step/t[n-1])
Plotando agora para diferentes condições através da biblioteca matplotlib, podemos observar os seguintes resultados á se comparar com resultados de medições diretas de tempos de tunelamento, como prometemos no final da sessão anterior:
plt.plot(t,phi)
plt.title("Analitycal tunneling time",fontsize = 16)
plt.xlabel("$t$", fontsize = 12)
plt.ylabel("$| \phi(t) |^2$", fontsize = 12)
plt.show()
Nossa inteção agora se volta para propor uma solução analítica para a equação (5.6). Esse problema já foi analisado de diferentes formas, e mostrou-se que para problema de uma partícula livre, existe uma forma fechada para sua solução ref. sessão 2.4. Agora, vamos mostrar que para uma vasta gama de sistemas físicos, os quais estão sob ação de um potencial independente do tempo, é possível usar uma técnica similar para obter uma solução geral. Relembrando que:
$$\sqrt{2m} \hat{\sigma_z} [i \hbar \frac{\partial}{\partial t} - V(T,x)]^{1/2} \phi (t|x) = -i \hbar \frac{\partial}{\partial x} \phi (t|x) $$
De maneira análoga a referência para solução da partícula livre, podemos usar uma separação de variáveis $\phi(t|x) = e^{-i\epsilon t/ \hbar} \phi_\epsilon (x)$, e pelo mesmo argumento da expansão em série vemos que
$$\hat{\sigma_z} \sqrt{2m [\epsilon - V(x)]} \phi_\epsilon (x) = -i \hbar \frac{d}{dx} \phi_\epsilon (x) \tag{7.1}$$
Esta é uma equação diferencial de primeira ordem cuja solução é dada por
$$\phi_\epsilon (x) = \frac{1}{\sqrt{2 \pi \hbar}} e^{(i/\hbar)\hat{\sigma_z} \int_{0}^{x} \sqrt{2m [\epsilon - V(x)]} dx^{\prime}} \tag{7.2}$$
Portanto, como (7.2) ainda é uma equação linear, podemos escrever a solução geral de forma que
$$\phi (t|x) = \frac{1}{\sqrt{2 \pi \hbar}} \int d\epsilon C_\epsilon e^{(i/\hbar)\hat{\sigma_z} \int_{0}^{x} \sqrt{2m [\epsilon - V(x)]} dx^{\prime}-i\epsilon t /\hbar} \tag{7.3}$$
Ou, em termos do momento clássico $P(\epsilon, x) = \pm \sqrt{2m\epsilon} $
$$ \phi (t|x) = \frac{1}{\sqrt{2 \pi \hbar}} \int d\epsilon C_\epsilon e^{(i/\hbar) \int_{0}^{x} P(\epsilon; x^{\prime}) dx^{\prime}-i\epsilon t /\hbar} \tag{7.4}$$
No intuito de resolver então analíticamente para qualquer potencial $V(x)$ basta realizar a integração no argumento da exponencial para obter a solução geral do problema. À primeira vista, essa simplicidade pode parecer estranha, afinal, para a equação de Schrödinger não temos uma solução com formato único para todo $V(x)$. Entretanto, este resultado é de certa forma esperado: primeiramente, analisando a Eq. (5.6), vemos que o potencial $V(x,t) = V(x)$ que escolhemos só depende do parâmetro condicional dessa equação, ou seja, da posição $x$. Dessa forma, se desejamos obter um resultado equivalente na equação de Schrödinger devemos escolher um potencial $V(x,t)$ que só dependa do parametro condicional t dessa equação, assim vamos encontrar o mesmo resultado na construção simétrica da mecânica quântica.
Prosseguindo na solução, vamos considerar primeiramente o caso mais simples como sendo o de uma partícula livre, onde o potencial será então dado por $V(x) = 0$. Se aplicarmos então essas condições a equação (7.3) e considerarmos apenas o ramo positivo da matriz de soluções $\hat{\sigma_z}$ vamos reduzir a mesma para
$$\phi (t|0) = \frac{1}{\sqrt{2 \pi \hbar}} \int d\epsilon C_\epsilon e^{(-i \epsilon t/\hbar)} \tag{7.5} $$
Note aqui que agora vamos prosseguir de forma muito semelhante ao que é feito na construção tradicional da teoria quântica, com o objetivo agora de evoluir espacialmente através da transformada de fourier a função de onda espaço condicional da nossa teoria
Tomando $$\phi (t|0) = \frac{1}{\sqrt{2 \pi \hbar}} \exp{\left[\frac{-(t-t_0)^2}{2 \sigma^2} \right]} \exp{\left[\frac{i \epsilon_0 t}{\hbar} \right]} \tag{7.6}$$
Como condição inicial, onde perceba que setei uma gaussiana de desvio padrão $\sigma$ em $x=0$, seguimos aplicando a transformada de Fourier já substituindo para a coordenada $\epsilon$ de forma que
$$\phi(t|0) = \int_{-\infty}^{\infty} \frac{d \epsilon}{\sqrt{2 \pi \hbar}} \psi(\epsilon) e^{i \epsilon t} \tag{7.7} $$
$$\psi(\epsilon) \equiv C_\epsilon = \int_{-\infty}^{\infty} \frac{1}{\sqrt{2 \pi\hbar} } \left ( \frac{1}{\sqrt{2\pi \hbar}} e^{-(t-t_0)^2/(2 \sigma^2)} e^{(i \epsilon_0 t)/\hbar} \right ) e^{-i\epsilon t} dt$$
$$= \frac{1}{ 2 \pi \hbar} \int_{-\infty}^{\infty} \left ( e^{-(t-t_0)^2/(2 \sigma^2)} e^{(i \epsilon_0 t)/\hbar} \right ) e^{-i \epsilon t} dt$$
$$ = \frac{1}{ 2 \pi \hbar} \frac{\exp{\left ( - \frac{(\epsilon_0 + \hbar \epsilon)\left ( \sigma^2(\epsilon_0 + \hbar \epsilon)-2i \hbar t_0 \right ) }{2 \hbar^2} \right )}}{\sqrt{\frac{1}{\sigma^2}}}$$
$$= \frac{\sigma^2}{ 2 \pi \hbar} \exp{\left ( - \frac{(\epsilon_0 + \hbar \epsilon)\left ( \sigma^2(\epsilon_0 + \hbar \epsilon)-2i \hbar t_0 \right ) }{2 \hbar^2} \right )} \tag{7.8}$$
O que isso nos diz é que a função de onda temporal da gaussiana é uma superposição de diferentes energias, com a probabilidade de achar essas energias entre $\epsilon_1$ e $\epsilon_1 + d \epsilon$ sendo proporcional a $ \exp{\left ( - \frac{(\epsilon_0 + \hbar \epsilon)\left ( \sigma^2(\epsilon_0 + \hbar \epsilon)-2i \hbar t_0 \right ) }{2 \hbar^2} \right )} d\epsilon$. A nível de recordação, vale relembrar o desenvolvimento desse problema dentro do escopo da teoria tradicional, procedendo da mesma forma e aplicando uma transformada de fourier numa gaussiana e obtendo outra gaussiana. Perceba aqui que os resultados obtidos são, assim como propostos, simétricos e equivalentes. Vamos pontuar também que a nossa função de onda inicial (7.4) que representa a solução encontrada para a equação de Schroedinger espaço condicional representa uma superposição de diferentes ondas planas associadas a diferentes coeficientes (que usualmente nos referimos como amplitudes).
Agora, finalmente de posse dos coeficientes $C_\epsilon$ podemos substituir de volta os resultados em (7.5) e obter o resultado da função de onda espaço-condicional dada uma condição de contorno espaço-inicial gaussiana.
Como também temos o resultado geral para $\phi(t|x)$ no caso da partícula livre, podemos substituir em (7.4) o valor encontrado para $C_\epsilon$ e entender como a função de onda irá se propagar em um instante de tempo t, dado que iremos observar ela em um espaço conhecido x.
$$\phi (t|0) = \frac{1}{\sqrt{2 \pi \hbar}} \int d\epsilon \frac{\sigma^2}{ 2 \pi \hbar} \exp{\left ( - \frac{(\epsilon_0 + \hbar \epsilon)\left ( \sigma^2(\epsilon_0 + \hbar \epsilon)-2i \hbar t_0 \right ) }{2 \hbar^2} \right )} e^{(-i \epsilon t/\hbar)}$$
$$= \frac{\sigma^2}{(2 \hbar \pi )^{3/2}} \int d\epsilon \exp{\left ( - \frac{(\epsilon_0 + \hbar \epsilon)\left ( \sigma^2(\epsilon_0 + \hbar \epsilon)-2i \hbar t_0 \right ) }{2 \hbar^2} \right )} e^{(-i \epsilon t/\hbar)} $$
onde $\text{erf}$ representa a função erro da gaussiana. Substituindo os limites de integração de menos infinito(?) até mais infinito, vamos obter
$$ \phi (t|0) = \frac{\sigma^2}{(2 \hbar \pi )^{3/2}} \left[ \dfrac{\sqrt{2}\sqrt{{\pi}}\mathrm{i}\mathrm{e}^{-\frac{t^2}{2\sigma^2 \hbar^2}+\frac{t_0 t}{\sigma^2\hbar}-\frac{t_0^2}{2\sigma^2}}\sin\left(\frac{\epsilon_0 t}{\hbar^2}\right)}{\sigma}+\dfrac{\sqrt{2}\sqrt{{\pi}}\mathrm{e}^{-\frac{t^2}{2\sigma^2 \hbar^2}+\frac{t_0 t}{\sigma^2\hbar}-\frac{t_0^2}{2\sigma^2}}\cos\left(\frac{\epsilon_0 t}{\hbar^2}\right)}{\sigma} \right]$$
$$ = \frac{\sigma}{(2 \hbar \pi )^{3/2}} \sqrt{2\pi} \mathrm{e}^{-\frac{t^2}{2 \sigma^2 \hbar^2}+\frac{t_0 t}{\sigma^2 \hbar}-\frac{t_0^2}{2\sigma^2}}\left(\mathrm{i}\sin\left(\frac{\epsilon_0 t}{\hbar^2}\right)+\cos\left(\frac{\epsilon_0 t}{\hbar^2}\right)\right) \tag{7.10}$$
Para auxiliar na visualização do sistema, segue o plot dessa função de onda em x = 0:
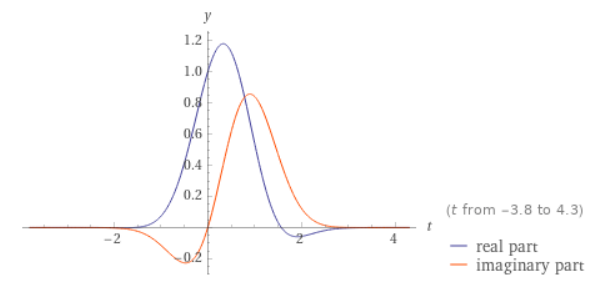
$$|\phi(t|0)|^2 = \frac{\sigma^2}{(2 \hbar \pi )^{3}} \dfrac{2{\pi}\mathrm{e}^{2\mathcal{Re}\left(-\frac{t^2}{2\sigma^2\hbar^2}+\frac{t_0t}{\sigma^2\hbar}-\frac{t_0^2}{2\sigma^2}\right)}\left|\mathrm{i}\sin\left(\frac{\epsilon_0 t}{\hbar^2}\right)+\cos\left(\frac{\epsilon_0 t}{\hbar^2}\right)\right|^2}{\sigma^2} = \frac{2{\pi}\mathrm{e}^{2\mathcal{Re}\left(-\frac{t^2}{2\sigma^2\hbar^2}+\frac{t_0t}{\sigma^2\hbar}-\frac{t_0^2}{2\sigma^2}\right)}\left|\mathrm{i}\sin\left(\frac{\epsilon_0 t}{\hbar^2}\right)+\cos\left(\frac{\epsilon_0 t}{\hbar^2}\right)\right|^2}{(2 \hbar \pi )^{3}} \tag{7.11}$$
Observe que até aqui, o resultado segue coerente visto que nossa expressão continua fazendo juz a gaussiana da condição inicial:
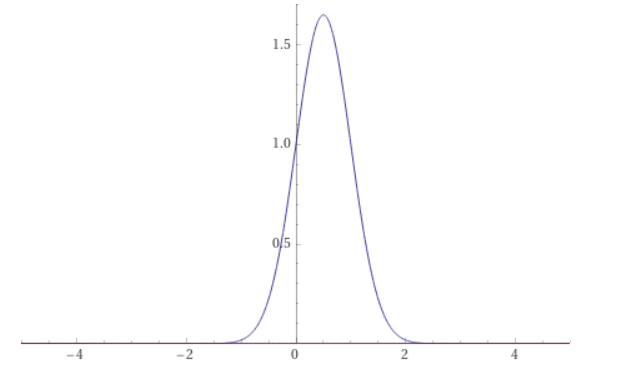
$$ \phi (t|x) = \frac{1}{\sqrt{2 \pi \hbar}} \int d\epsilon \frac{\sigma^2}{ 2 \pi \hbar} \exp{\left ( - \frac{(\epsilon_0 + \hbar \epsilon)\left ( \sigma^2(\epsilon_0 + \hbar \epsilon)-2i \hbar t_0 \right ) }{2 \hbar^2} \right )} e^{(i/\hbar) \sqrt{2m\epsilon} x-i\epsilon t /\hbar } $$
$$=\frac{\sigma^4}{(2 \hbar \pi )^{3/2}} \int d\epsilon \exp{\left ( - \frac{(\epsilon_0 + \hbar \epsilon)\left ( \sigma^2(\epsilon_0 + \hbar \epsilon)-2i \hbar t_0 \right ) }{2 \hbar^2} \right )} e^{(i/\hbar) \sqrt{2m\epsilon} x-i\epsilon t /\hbar}$$
$$\text{(note que ela não divergiu, apenas não tem solução analítica. Integrando numericamente para todas as constantes = 1 obtemos para a condição inicial: 1.390521824852123 + 0.2928372699906291 i)} $$
No intuito de eliminar a raíz do expoente que nos impossibilita essa integração, podemos então utilizar da construção de $\epsilon$ que como $P = \pm \sqrt{2 m \epsilon}$, isto é, $ \epsilon_p = P^2/2m $. Efetuando essa substituição vamos obter que:
$$\epsilon_p = \frac{P^2}{2m} \Rightarrow d\epsilon = \frac{P}{m} dP \tag{7.12}$$
Então, procedendo com a integração de 0 até $\infty$ (ao substituir o $P^2$ do expoente de $C_P$
$$ \phi (t|x) = \frac{1}{\sqrt{2 \pi \hbar}} \int dP \frac{P }{ m} \frac{\sigma^2}{ 2 \pi \hbar} \exp{\left ( - \frac{(P_0 + \frac{\hbar P^2}{2 m})\left ( \sigma^2(P_0 + \frac{\hbar P^2}{2 m})-2i \hbar t_0 \right ) }{2 \hbar^2} \right )} e^{(i/\hbar) P x - i P^2 t /2 m \hbar } $$
$$\phi (t|x) = \frac{\sigma^2}{ (2 \pi \hbar)^{3/2} m} \int dP P\exp{\left ( - \frac{(P_0 + \frac{\hbar P^2}{2 m})\left ( \sigma^2(P_0 + \frac{\hbar P^2}{2 m})-2i \hbar t_0 \right ) }{2 \hbar^2} \right )} e^{(i/\hbar) P x - i P^2 t /2 m\hbar } $$
Observação: continuarei de forma analítica aqui, todavia fui capaz de resolver/plotar computacionalmente a integral acima; posso então trabalhar em gráficos complementares analiticos/computacionais a partir disso
Setando o instante de tempo inicial $t_0$ como zero da nossa condição inicial gaussiana temporal, podemos simplificar nossa integral sem perder nenhum tipo de generalidade ou aplicação do problema, podendo então escrever a expressão como
$$ \phi (t|x) = \frac{\sigma^2}{ (2 \pi \hbar)^{3/2} m} \int dP P\exp{\left ( - \frac{ \sigma^2(P_0 + \frac{\hbar P^2}{2 m})^2 }{ 2 \hbar^2} \right )} e^{(i/\hbar) P x - i P^2 t /2 m\hbar }\tag{7.13}$$
Considerando a energia inicial como sendo $\epsilon_0 = 0$, isso nos leva de $\epsilon_0 = P_0^2/2m$ em $P_0 = 0$, que simplifica nossa integral mais uma vez em:
$$\phi (t|x) = \frac{\sigma^2}{ (2 \pi \hbar)^{3/2} m} \int dP P\exp{\left ( - \frac{\sigma^2 \hbar^4 P^4}{ m} \right )}e^{ - i P^2 t /2 m\hbar } e^{(i/\hbar) P x} \tag{7.14}$$
$$ \left ( - \frac{\sigma^2 P^2}{ 2m\hbar} \right ) - \frac{i P^2 t }{2 m} = -\frac{b P^2}{2} $$
tomando $ b = \frac{1}{m \hbar} \left ( \sigma^2 + i t \right )$, podemos simplificar ambas as exponenciais para
$$\phi (t|x) = \frac{\sigma^2}{ (2 \pi \hbar)^{3/2} m} \int dP P e^{-\frac{b P^2}{2}} e^{(i/\hbar) P x} $$
cujo resultado da integral acima sabemos de integrais tabeladas como sendo:
$$ I = \frac{1}{b} - \frac{\sqrt{\frac{\pi}{2}} x e^{-x^2/(2 b^2)} \left( \text{erfi} \left( \frac{x}{\sqrt{2 b}} \right) - i\right) }{b^{3/2}}$$
Fazendo então com que o resultado da função de onda espaço evoluída seja
$$\phi (t|x) = \frac{\sigma^2}{ (2 \pi \hbar)^{3/2} m} \left[ \frac{m \hbar}{\sigma^2 + it} - \frac{\sqrt{\frac{\pi}{2}} (m \hbar)^{3/2} x e^{-\frac{x^2 (m\hbar)^2}{(2 (\sigma^2+it)^2)}} \left( \text{erfi} \left( x \sqrt{\frac{\sigma^2 + it }{2 m \hbar}} \right) - i\right) }{(\sigma^2 + it)^{3/2}} \right] \tag{7.14-1}$$
(Tenho plots para mostrar tanto da função de onda quanto da densidade de probabilidade - posso mostrar 1 a 1, a animação ainda não tive tempo de implementar para vocês poderem visualizar a evolução)
Com respectiva densidade de probabilidade :
$$|\phi(t|x)|^2 = \frac{\sigma^4}{ (2 \pi \hbar)^{3}m^2 } \left[ \dfrac{\left(bx\mathrm{e}^\frac{x^2}{\mathrm{i}t+\sigma^2}\operatorname{erfi}\left(x\sqrt{\mathrm{i}t+\sigma^2}\right)-hm\sqrt{\mathrm{i}t+\sigma^2}-\mathrm{i}\right)^2}{\left|\mathrm{i}t+\sigma^2\right|^3} \right] \tag{7.15}$$
Para efeito de visualização, segue um plot do formato geral da função de onda evoluída em x = 1, utilizando 1 para todas as constantes e evoluindo ela numericamente em t:
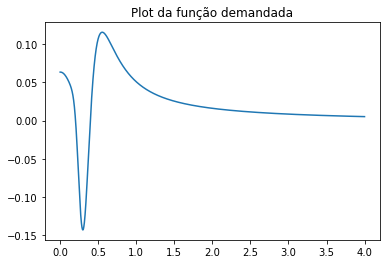
segue também o plot da densidade de probabilidade na posição x = 1,
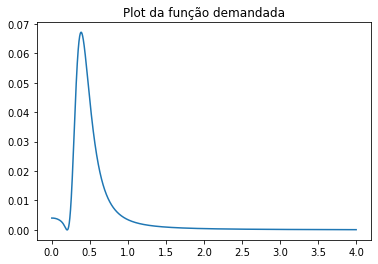
Note aqui que utilizamos embutido no resultado espacialmente evoluído a ideia de um propagador espacial para o sistema no intuito de obter $ \phi (t|x)$. A nível de curiosidade, vou desenvolver de forma geral a ideia de um propagador no escopo da teoria espelhada, e obter um resultado coerente com o que podemos observar em (7.10): para $x_0 = 0$, o propagador se torna $e^{(i/\hbar)\sqrt{2m \epsilon} x} $.
Perceba também que o termo da transformada $\exp (i\epsilon t)$, está associado para cada coeficiente $C_\epsilon$ com uma autofunção do nosso novo Pamiltoniano com autovalor em forma de $E_\epsilon = \sqrt{2 m \epsilon}/ \hbar$. Logo, nós sabemos que $\exp (i\epsilon t)$ deve evoluir no espaço com uma dependência espacial dada por $e^{-iE_\epsilon x /\hbar}$, devido ao formato do nosso Pamiltoniano, como mostraremos à seguir
Na intenção de examinar como um estado irá evoluir espacialmente, vamos restabelecer a definição de um propagador em nossa nova teoria como sendo um operador linear escrito como $\hat{U}(x,x_0)$, tal que
$$|\phi(x) \rangle = \hat{U}(x,x_0) |\phi(x_0) \rangle \tag{a.1}$$
podemos também inferir a seguinte propriedade:
$$\hat{U}(x_0,x_0) = \hat{I} \tag{a.2}$$
onde $\hat{I}$ é o operador unidade (identidade)
No propósito de avançar no que haviamos proposto anteriormente, precismos encontrar a forma analítica desse operador $\hat{U}(x,x_0)$, para isso, vamos simplesmente substituí-lo (7.9) na relação do Pamiltoniano de (4.14), isto é
$$ \mathcal{\hat{P}} \left ( \hat{U}(x,x_0)|\phi(x_0) \rangle \right ) = -i\hbar \frac{\partial }{\partial x} \left ( \hat{U}(x,x_0)|\phi(x_0) \rangle \right ) \tag {a.3}$$
ou,
$$\frac{\partial \hat{U}(x,x_0)}{\partial x} = \frac{i}{\hbar} \hat{P} \hat{U}(x,x_0) \tag{a.4}$$
Assumindo o Pamiltoniano espaço independente podemos proceder de forma parecida a MQ tradicional e integrar facilmente essa equação diferencial de forma a obter que
$$\boxed{\hat{U}(x,x_0) = e^{i(x-x_0)\hat{P}/\hbar} \longmapsto e^{i(x-x_0) \sqrt{2m\epsilon}/\hbar}} \tag{a.5}$$
A partir de agora, usaremos esse operador propagador de forma equivalente ao que fazemos para operar evoluções temporais na MQ tradicional, todavia, o faremos agora para evoluções espaciais no escopo da teoria espelhada.
Agora, seguindo em diante com o resultado encontrado, vamos verificar se o mesmo encontra-se tempo normalizado. Para isso, vamos analisar
$$ \int_{-\infty}^{\infty} |\phi(t|x)|^2 dt = 1 \tag{7.16}$$
Como ainda não resolvemos a questão da integração para a função de onda espaço evoluída, vamos analisar o caso condicionla de $x = 0$ que já podemos normalizar no tempo. Prosseguindo com:
$$ \int_{-\infty}^{\infty} |\phi(t|0)|^2 dt = 1 \tag{7.17}$$
$$1 = \int_{-\infty}^{\infty} \frac{2{\pi}\mathrm{e}^{2\mathcal{Re}\left(-\frac{t^2}{2\sigma^2\hbar^2}+\frac{t_0t}{\sigma^2\hbar}-\frac{t_0^2}{2\sigma^2}\right)}\left|\mathrm{i}\sin\left(\frac{\epsilon_0 t}{\hbar^2}\right)+\cos\left(\frac{\epsilon_0 t}{\hbar^2}\right)\right|^2}{(2 \hbar \pi )^{3}} dt \tag{7.18}$$
assumindo então $ \sigma, \hbar, \epsilon_0, t, t_0$ como reais podemos escrever nossa integral para a forma:
$$ \frac{\sigma^2}{(2 \hbar \pi )^{3}} \int_{-\infty}^{\infty} \dfrac{2{\pi}\mathrm{e}^{-\frac{t^2}{\sigma^2\hbar^2}+\frac{2t_0t}{\sigma^2 \hbar}-\frac{t_0^2}{\sigma^2}}}{\sigma^2} dt \tag{7.19}$$
Contraindo os termos do expoente no formato de quadrado da soma, pode convenientemente nos ajudar a enchergar uma função de erro de gauss, isto é:
$$ \frac{\sigma^2}{(2 \hbar \pi )^{3}} \int_{-\infty}^{\infty} \dfrac{2{\pi}\mathrm{e}^{-\frac{\left(t-t_0 \hbar \right)^2}{\sigma^2 \hbar^2}}}{\sigma^2} dt \Rightarrow \frac{\sigma^4}{(2 \hbar \pi )^{3}} \dfrac{{\pi}^\frac{3}{2}\hbar \operatorname{erf}\left(\frac{t}{\sigma \hbar}-\frac{t_0}{\sigma}\right)}{\sigma} \tag{7.20}$$
Substituindo os limites de integração, podemos então facilmente ver que
$$ \int_{-\infty}^{\infty} |\phi(t|0)|^2 dt = \frac{\sigma^2}{(2 \hbar \pi )^{3}} \dfrac{2{\pi}^\frac{3}{2}\hbar}{\sigma} = \frac{\sigma}{4 \hbar^2 \pi^{3/2}} \tag{7.21}$$
Logo, a constante de normalização pode ser simplesmente expressada através de $4 \hbar^2 \pi^{3/2}/\sigma$.
import cmath
i = 0 + 1j
print('e^i =', cmath.exp(i))
print (i)
def f(x):
return x**2
print('f', x)
(-1) ** 0.5
import quadpy
import math as math
from math import e
from math import pi
from math import sqrt
import numpy as np
from scipy import integrate
import matplotlib.pyplot as plt
import cmath
from scipy.optimize import fmin
#definindo unidade imaginária:
i = 0 + 1j
#criando a função para o plot
def plot_results(sigma = 1, Xp = 1, m=1, P_0 = 1, hbar = 1):
#preparando a função que vai ser integrada para a integração
def f(x, t):
res = (sigma**2)/(2*pi*hbar)**(3/2)*x*e**(-(P_0 + hbar*(x**2)/(2*m))*(sigma**2)*(P_0 + hbar*(x**2)/(2*m))/(2*hbar**2))*cmath.exp((i/hbar)*x*Xp - i*(x**2)*t/(2*m*hbar))
return res
integral = np.vectorize(f)
#efetuando a integral
def F(t):
xmin = 0
xmax = 10
y,err = quadpy.quad(lambda x: integral(x,t), xmin, xmax)
return y
Fvec = np.vectorize(F)
"""
def piu(x):
return fmin(Fvec, 0, args=(x))
#print('piu', x)
"""
return Fvec
X0 = plot_results(1,0,1,1,1)
X1 = plot_results(1,5,1,1,1)
X2 = plot_results(1,10,1,1,1)
X3 = plot_results(1,15,1,1,1)
t = np.linspace(-5,40,200)
plt.plot(t, abs(X0(t))**2, label='x=0')
plt.plot(t, abs(X1(t))**2, label='x=5')
plt.plot(t, abs(X2(t))**2, label='x=10')
plt.plot(t, abs(X3(t))**2, label='x=15')
plt.legend()
plt.title('Numerical evolution of the probability density of Gaussian wave packet')
plt.ylabel('$|\phi(t|x)|^2$')
plt.xlabel('$t$')
from scipy.integrate import quad
from math import exp, cos, sin, pi, sqrt
import numpy as np
import matplotlib.pyplot as plt
#defina aqui as constantes:
sigma = 1
hbar = 1
m = 1
P_0 = 0
i = 0 + 1j
x = 8
#preparando a função que vai ser integrada para a integração, dividida em real e imaginária
#parte real:
def re(p, t):
RE = (sigma**2)/(2*pi*hbar)**(3/2)*p*exp(-(P_0 + hbar*(p**2)/(2*m))*(sigma**2)*(P_0 + hbar*(p**2)/(2*m))/(2*hbar**2))*cos((1/hbar)*p*x - 1*(p**2)*t/(2*m*hbar))
return RE
integral1 = np.vectorize(re)
#parte imaginária
def im(p, t):
IM = (sigma**2)/(2*pi*hbar)**(3/2)*p*exp(-(P_0 + hbar*(p**2)/(2*m))*(sigma**2)*(P_0 + hbar*(p**2)/(2*m))/(2*hbar**2))*sin((1/hbar)*p*x - 1*(p**2)*t/(2*m*hbar))
return IM
integral2 = np.vectorize(im)
#efetuando a integral em p e passando t para ser o argumento da função de onda
def F(t):
min = 0
max = 10
y, err = quad(integral1, min, max, args=(t))
return y
def M(t):
min = 0
max = 10
y, err = quad(integral2, min, max, args=(t))
return y
def OP(t):
return abs(F(t) + M(t)*i)**2
OPvec = np.vectorize(OP)
t = np.linspace(-0,20,200)
plt.plot(t, OPvec(t))
plt.title('Numerical evolution of the probability density of Gaussian wave packet')
plt.ylabel('$|\phi(t|x)|^2$')
plt.xlabel('$t$')
from scipy.integrate import quad
from math import exp, cos, sin, pi
import numpy as np
import matplotlib.pyplot as plt
#defina aqui as constantes:
sigma = 1
hbar = 1
m = 1
P_0 = 0
i = 0 + 1j
n = 15
irio = 100
piu = np.zeros(irio)
valor_x = np.zeros(n)
maximum = np.zeros(n)
tuntime = np.zeros(n)
x = 5
#preparando a função que vai ser integrada para a integração, dividida em real e imaginária
#parte real:
def re(p, t):
RE = (sigma**2)/(2*pi*hbar)**(3/2)*p*exp(-(P_0 + hbar*(p**2)/(2*m))*(sigma**2)*(P_0 + hbar*(p**2)/(2*m))/(2*hbar**2))*cos((1/hbar)*p*x - 1*(p**2)*t/(2*m*hbar))
return RE
integral1 = np.vectorize(re)
#parte imaginária
def im(p, t):
IM = (sigma**2)/(2*pi*hbar)**(3/2)*p*exp(-(P_0 + hbar*(p**2)/(2*m))*(sigma**2)*(P_0 + hbar*(p**2)/(2*m))/(2*hbar**2))*sin((1/hbar)*p*x - 1*(p**2)*t/(2*m*hbar))
return IM
integral2 = np.vectorize(im)
#efetuando a integral em p e passando t para ser o argumento da função de onda
def F(t):
min = 0
max = 20
y, err = quad(integral1, min, max, args=(t))
return y
def M(t):
min = 0
max = 20
y, err = quad(integral2, min, max, args=(t))
return y
def OP(t):
return abs(F(t) + M(t)*i)**2
OPvec = np.vectorize(OP)
#integrando em t para obter a função de normalização
def norm(t):
min = -20
max = 20
y, err = quad(OPvec, min, max)
return y
#normalizando
def graph(t):
return OP(t)/norm(t)
graph_vec = np.vectorize(graph)
for k in range (irio):
piu[k] = graph(k)
tuntime = np.argmax(piu)
print(tuntime)
maximum = np.amax(piu)
print(maximum)
#organizando o plot da função em questão
t = np.linspace(-5,15,200)
plt.scatter(t, graph_vec(t), s = 2)
plt.ylabel('$|\phi(t|x)|^2$')
plt.xlabel('$t$')